
zk-SNARKs
*unfinished*
What are SNARKs for?
SNARKs, and zero-knowledge proofs in general, allow for a party to compute heavy computation on chain and then present an easy to verify proof on chain.
What is a SNARK?
A SNARK is a Succinct Non-Interactive ARgument of Knowledge.
Succinct means that the SNARK itself, aka the proof, is shorter than the actual witness that is being proved; it is typically at least O(log n) shorter.
Non-Interactive means that in order for the Verifier to verify the proof, they do not need to communicate back and forth with the Prover that has presented the proof. All they need is the proof itself and a public algorithm.
Arguments of Knowledge implies the proof is related to some boolean or quantitative value.
A zk-SNARK is a SNARK that reveals no information about the situation to the verifier; this is why it is a zero-knowledge SNARK. A SNARK on its own is an excellent tool to save memory and computation by only needing to confirm a small value to validate a larger set of data (similar to comparing Merkle roots), but adding the zk aspect adds privacy too.
Zk-SNARKs allow the witness to be secret, shorten proofs, and allow for faster verification.
Size and verify time are both O(log n)
Setup Procedures
Trusted setup per circuit: Setup of Circuit, S(C), uses data that must be kept secret. Data must be destroyed after the setup is completed to maintain security.
Types of SNARKs
Kilian92, Micali94: verifier time is great but prover time is too slow
Groth16: linear prover and constant sized proof. Requires trusted setup.
PLONK, Sonic, Marlin: universal trusted setup
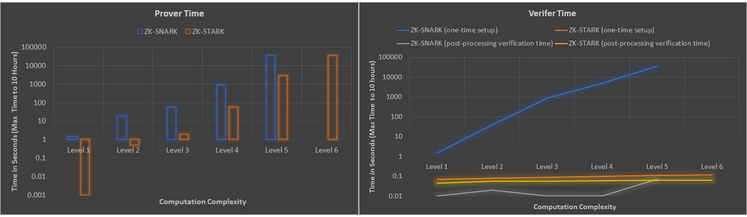
STARKs
STARKs are Scalable Transparent Arguments of Knowledge.
Scalable because proving/verifying complexity is quasilinear unlike SNARKs in which computation increases linearly
No trusted setup, Transparent because they use publicly verifiable randomness to set up interactions between provers and verifiers.
Proof is larger than SNARKs, they’re not as succinct.
Bulletproofs
Transparent setup, and a short proof compared to other transparent setups. Bulletproofs are an improvement on range proofs. Applying zk proofs to range proofs, the size of the proof is dramatically reduced; this allows for them to obfuscate transaction amounts without clogging the network.
Bulletproofs also do not require a trusted setup, which is vital for their use case of obfuscating single transactions.
A drawback is that they have slow verifier time (linear rather than logarithmic).
Let's Compare
Size of proof π | Size of setup Sₚ | Verifier time | Trusted setup? | |
Groth16 | O(1) | O(|C|) | O(1) | Per circuit |
PLONK/Marlin | O(1) | O(|C|) | O(1) | Universal |
Bulletproofs | O(log|C|) | O(1) | O(|C|) | no |
STARK | O(log|C|) | O(1) | O(log|C|) | no |
DARK | O(log|C|) | O(1) | O(log|C|) | no |
References:
Dan Boneh

