Diffie-Hellman Key Exchange (DHKE)

Diffie-Hellman key exchange is a method for securely agreeing on a shared key between two communication partners. DHKE is a combination of asymmetric and symmetric encryption techniques; an asymmetric algorithm is used to establish the symmetric key/shared secret key. This method allows for two parties to combine their secret keys into a shared key without ever actually knowing each other's secret key.

Protocols using DHKE include:

• ZKP (zero-knowledge proof)
• SSH (secure shell)
• TLS (transport layer security)
• SSL (secure sockets layer)
• Signal (messenger apps like FB, Signal, WhatsApp)

How It Works

For Alice and Bob to create a secure, shared secret key they must complete a few messages. Some of that data will be public and accessible to any adversaries, but the final product cannot be derived from the public pieces.

Variables: The level of security is directly correlated to the size of 'n'. n is typically in the size range of 2000-4000 bits. There is a trade-off between security (larger n is more secure) and efficiency (smaller n is more efficient to compute) with this variable.

• g - a public prime number, used as a generator, typically a small number
• n - a public prime number, used as an upper-limit, typically much larger

• a - a number between 1 and n, Alice's private key only known by themself

• b - a number between 1 and n, Bob's private key only known by themself

Equations:

• 1. gᵃ % n = A

• 2. gᵇ % n = B
• 3. Bᵃ = ((g)ᵇ)ᵃ = gᵇᵃ = S (shared secret)
• 4. Aᵇ = ((g)ᵃ)ᵇ = gᵃᵇ = S (shared secret)
• gᵃᵇ = gᵇᵃ
• 5. (B)ᴬ = (((g)ᵇ)ᵍ)ᵃ = gᵇᵍᵃ != S
• 6. (A)ᴮ = (((g)ᵃ)ᵍ)ᵇ = gᵃᵍᵇ != S
• gᵃᵇᵍ != gᵃᵇ

Note: equations 3-6 don't include 'modulo n' for better readability of the exponents. This is what the proper equations look like:

• 3. Bᵃ % n = ((g)ᵇ)ᵃ % n = gᵃᵇ % n = S
• 4. Aᵇ % n = ((g)ᵃ)ᵇ % n = gᵃᵇ % n = S
• 5. (B)ᴬ % n = (((g)ᵇ)ᵍ)ᵃ % n = gᵇᵍᵃ % n != S
• 6. (A)ᴳ % n = (((g)ᵃ)ᵍ)ᵇ % n = gᵃᵍᵇ % n != S

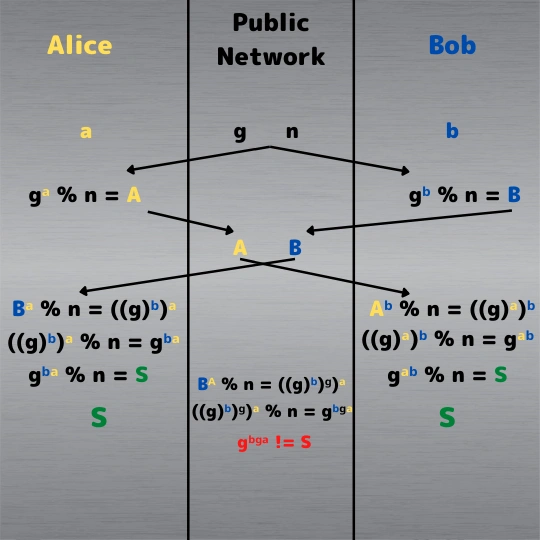
Alice and Bob both calculate 'g' to the power of their respective private key, modulo 'n'; resulting in equations 1 and 2. The resulting values A and B, respectively, will always be between 0 and n because of the 'modulo n' part of the equation.

The values A and B can be freely sent between Alice and Bob as plaintext because 'a' and 'b' cannot be derived from the values. The only way for anyone other than Alice (any adversary or even Bob) to derive 'a' is for them to brute force gᵃ%n working backward from A.

With A and B now being public knowledge, they can take each other's public values and combine their own private key. Alice would raise B to the 'a' power mod 'n', and Bob would raise A to the 'b' power mod 'n'. See equations 3 and 4.

Alice and Bob now have a shared secret key, a symmetric key, known as S, that has been derived from their personal private keys. While incomplete versions of the key exist in plaintext, that public information can't be used to derive the final shared secret key, as shown in equations 5 and 6.